(NM)

(NN)

(NC)

(N2)

(NB)

(ND)

(N+)

(NX)

(N*)

(N#)

Larger than Life (LtL) is a family of cellular automata rules that generalize John Conway's Game of Life to large neighborhoods and general birth and survival thresholds.
Golly supports three different rule notations:
The first rule notation used by Golly is identical to the one created by Mirek Wojtowicz for MCell:
Rr - specifies the neighborhood range (r is from 1 to 500,
except for Triangular where r is from 1 to 250 and
Gaussian where r is from 1 to 50).
Cc - specifies the number of states (c is from 0 to 256).
Mm - specifies if the middle cell is included in the neighborhood count (m is 0 or 1).
Ssmin..smax - specifies the count limits for a state 1 cell to survive.
Bbmin..bmax - specifies the count limits for a dead cell to become a birth.
Nn - specifies the extended neighborhood type.
These diagrams show the supported neighborhoods, Nn, for r = 3:
Square grid:
| Type | Diagram | Type | Diagram | Type | Diagram |
|---|---|---|---|---|---|
| Moore (NM) |  |
von Neumann (NN) |  |
Circular (NC) |  |
| L2/Euclidean (N2) |  |
Checkerboard (NB) |  |
Aligned Checkerboard (ND) |  |
| Cross (N+) |  |
Saltire (NX) |  |
Star (N*) |  |
| Hash (N#) |  |
Hexagonal grid:
| Type | Diagram | Type | Diagram | Type | Diagram |
|---|---|---|---|---|---|
| Hexagonal (NH) |  | Asterisk (NA) |  |
Tripod (N3) |  |
Use hexgrid.lua or showinviewer.lua to view Hexagonal, Asterisk or Tripod neighborhoods on a hexagonal grid.
| Type | Diagram |
|---|---|
| Triangular (NL) |  |
The Triangular neighborhood flips the neighborhood vertically on alternating cells.
Use showinviewer.lua to view Triangular neighborhoods on a triangular grid.
Other supported neighborhoods:
Weighted allows you to specify a weight for each cell in the neighborhood. The neighbor count will be the sum of each alive cell's neighborhood position weight. Weights from -127 to 127 are supported.
The format is NW following by a string of hexadecimal digits to specify the neighbor weights.
The hexadecimal representation has the MSB as the sign bit which means:
Example (single digit):
becomes NW123401323
Example (double digits):
becomes NW0810080a850a081008
Following the neighborhood weights you can optionally specify state weights. In this case the neighbor count will be the sum of each live cell's neighborhood position weight multiplied by its state weight.
To specify state weights, add a comma after the NW neighborhood specification and then one hex digit per state. You must specify the same number of state weights as states in the pattern defined by the Cc parameter.
Allowed state weight values are 0 to 15 (decimal) which are specified as 0 to f (hexadecimal).
Example:
If you have a 4-state pattern and want state weights 0, 1, 2, 10 then you'd specify:
Finally, if you want a non-square grid you can add a suffix to the rule string of H for hexagonal grid or L for triangular grid. Triangular grid will cause weightings to be treated as a triangular neighborhood and flip vertically on alternating cells.
Gaussian defines a weighted neighborhood based on the defined range. Only square grids are allowed.
Example: R3,C2,M0,S24..31,B24..28,NG (r = 3)

You can specify a custom neighborhood using N@ and then hexadecimal digits. There are two ways to create the hexadecimal digits:
The easiest is to draw the custom neighborhood in Golly as a set of live cells. Surround the cells in a square selection and then run create-custom-ltl.lua to automatically create the rule string.
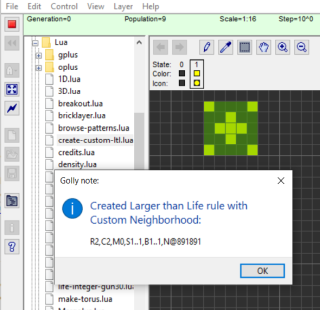
Alternatively you can create them manually, using the following method:
Rule becomes:
If you want a non-square grid you can add a suffix to the rule string of H for hexagonal grid or L for triangular grid. Triangular grid will cause the custom neighborhood to be treated as a triangular neighborhood and flip vertically on alternating cells.
The S and B limits must be from 0 to the neighborhood size. A quick way to see the neighborhood and get the limits for a given r and n is to use a rule with only B1 set. For example, switch to R6,C0,M0,S1..1,B1..1,NC, turn on a single cell and hit the space bar. The population count is the limit.
If the number of states (specified after C) is greater than 2 then states 1 and above don't die immediately but gradually decay. Note that state values above 1 are not included in the neighborhood counts and thus play no part in deciding the survival of a state 1 cell, nor the birth of an empty cell. The one exception to this is Weighted neighborhoods that have state weights defined. C0 and C1 are equivalent to C2.
The Patterns/Larger-than-Life folder contains a number of example patterns (mostly from the MCell collection). The following table shows a number of example rules along with their commonly used names:
| R1,C0,M0,S2..3,B3..3,NM | [Life] | - the default rule for this algorithm. | ||
| R5,C0,M1,S34..58,B34..45,NM | [Bosco's Rule] | - (aka Bugs) a chaotic rule by Kellie Evans. | ||
| R10,C0,M1,S123..212,B123..170,NM | [Bugsmovie] | - a chaotic rule by David Griffeath. | ||
| R8,C0,M0,S163..223,B74..252,NM | [Globe] | - an expanding rule by Mirek Wojtowicz. | ||
| R1,C0,M1,S1..1,B1..1,NN | [Gnarl] | - an exploding rule by Kellie Evans. | ||
| R4,C0,M1,S41..81,B41..81,NM | [Majority] | - a stable rule by David Griffeath. | ||
| R7,C0,M1,S113..225,B113..225,NM | [Majorly] | - an expanding rule by David Griffeath. | ||
| R10,C255,M1,S2..3,B3..3,NM | [ModernArt] | - a chaotic rule by Charles A. Rockafellor. | ||
| R7,C0,M1,S100..200,B75..170,NM | [Waffle] | - an expanding rule by Kellie Evans. |
The second notation used by Golly was defined by Kellie Evans in her thesis [2]. The range, birth limits and survival limits are specified by five integers separated by commas:
This notation assumes an extended Moore neighborhood in which a live middle cell is included in the neighborhood count (i.e. totalistic). For example, Life can be entered as 1,3,3,3,4.
Note that Golly's canonical version of Larger than Life rules defined with this notation will be in the LtL notation.
HROT (Higher Range Outer Totalistic) Notation
The third notation used by Golly is the HROT notation used by LifeViewer. It provides more flexibility than the previous two notations since it allows arbitrary definitions of birth and survival counts to be specified.
Rr - specifies the neighborhood range (r is from 1 to 500,
except for Triangular where r is from 1 to 250 and Gaussian where r is from 1 to 50).
Cc - specifies the number of states (c is from 0 to 256).
Slist - specifies the counts for a state 1 cell to survive.
Blist - specifies the counts for a dead cell to become a birth.
Nn - specifies the extended neighborhood type (and can be omitted for Moore).
It supports the same neighborhoods as specified above for LtL notation.
HROT differs from LtL in three ways:
The canonical form for a rule specified in HROT notation is also HROT.
The Larger than Life algorithm supports both bounded and unbounded universes, but with certain restrictions. As in Golly's other algorithms, a bounded universe is specified by appending a suitable suffix to the rule, but the topology can only be a simple torus or a plane. For example, R5,C0,M1,S34..58,B34..45,NM:T500,40 creates a 500 by 40 torus using Bosco's Rule, and 1,3,3,3,4:P300,200 creates a 300 by 200 plane using Life. The maximum grid size is 100 million cells. The minimum width or height is twice the supplied range. Values less than that (including zero) are automatically increased to the minimum value.
If a given rule has no suffix then the universe is unbounded. Well, almost. Golly maintains an internal grid that is automatically resized as a pattern expands or shrinks. The size of this grid is limited to 100 million cells, and the cell coordinates of the grid edges must remain within the editing limits of +/- 1 billion. For the vast majority of patterns these limits won't ever be a problem.
One more restriction worth noting: For 2-state patterns in both bounded and unbounded universes B0 is emulated to prevent pattern strobing. B0 is not supported in >2 state patterns.
Larger than Life was first imagined by David Griffeath in the early 1990s to explore whether Life might be a clue to a critical phase point in the threshold-range scaling limit [1]. The LtL family of rules includes Life as well as a rich set of two-dimensional rules, some of which exhibit dynamics vastly different from Life [2], [3]. Kellie Evans studied LtL in her 1996 thesis and discovered that a family of "Life-like" rules comprises a much larger subset of LtL parameter space than initially imagined [2], [4], [5].
In order to study LtL rules, David Griffeath and Bob Fisch developed WinCA, a cellular automata modeling environment for Windows. WinCA's editing capabilities were modest, but the software was able to implement LtL rules to range 200 and its speed increased together with the hardware on which it ran. In those early days of Windows, Griffeath's Primordial Soup Kitchen shared graphics and other discoveries via weekly "soup recipes" [6]. WinCA still runs on 32-bit Windows and allows for colorful LtL and other cellular automata images [10], [11]. Just before LtL was implemented in Golly, a virtual machine was used to run WinCA on 64-bit Windows and some new discoveries were made [12].
In 1999 Mirek Wojtowicz developed Mirek's Cellebration (MCell) [9], a cellular automata modeling environment for Windows, which was excellent for editing on the fly and working with small configurations for LtL rules up to range 10. Dean Hickerson used MCell to construct the first "bug gun" using the period 166 oscillator known as Bosco, which was discovered by Kellie Evans. This construction led to numerous other constructions and questions [7].
Golly is a game changer in the study of LtL: the first software with seemingly boundless possibilities that implements LtL in ranges up to 500 and the potential to discover LtL dynamics as yet unimagined.
[1] D. Griffeath. Self-organization of random cellular automata: Four snapshots, in "Probability and Phase Transitions", 1994. (G. Grimmett Ed.), Kluwer Academic, Dordrecht/Norwell, MA.
[2] K. Evans. "Larger than Life: it's so nonlinear", 1996. Ph.D. dissertation,
University of Wisconsin- Madison.
http://www.csun.edu/~kme52026/thesis.html
[3] J. Gravner and D. Griffeath. Cellular automaton growth on Z2: theorems, examples,
and problems, 1998. Advances in App. Math 21, 241-304.
http://psoup.math.wisc.edu/extras/r1shapes/r1shapes.html
[4] K. Evans. Larger than Life: digital creatures in a family of two-dimensional
cellular automata, 2001. Discrete Mathematics and Theoretical Computer Science,
Volume AA, 2001, 177-192
http://dmtcs.loria.fr/proceedings/html/dmAA0113.abs.html
[5] K. Evans, Threshold-range scaling of Life's coherent structures, Physica D 183 (2003), 45-67.
[6] D. Griffeath. Primordial Soup Kitchen.
http://psoup.math.wisc.edu/kitchen.html
[7] K. Evans, Is Bosco's rule universal?, in "Lecture Notes in Computer Science," Vol. 3354,
ed. Maurice Margenstern. Springer-Verlag GmbH (2005), 188–199. WWW companion page to paper
http://www.csun.edu/~kme52026/bosco/bosco.html
[8] K. Evans. Replicators and Larger than Life examples, 2002. In "New Constructions in Cellular Automata", eds. David Griffeath and Cris Moore. Oxford University Press.
[9] MCell rules lexicon for Larger than Life:
http://www.mirekw.com/ca/rullex_lgtl.html
[10] D. Griffeath. Self-organizing two-dimensional cellular automata: 10 still frames. In "Designing Beauty: the Art of Cellular Automata," eds. Andrew Adamatzky and Genaro Martinez. Springer (2016) 1-12.
[11] K. Evans. Larger than Life. In "Designing Beauty: the Art of Cellular Automata," eds. Andrew Adamatzky and Genaro Martinez. Springer (2016) 27-34.
[12] A. Tantoushian. "Scaling Larger than Life Bugs: to range 25 and beyond", 2017 Master's thesis,
California State University, Northridge.
http://scholarworks.csun.edu/handle/10211.3/192639